Bufory zadania – jak to ogarnąć i nie zwariować?

We wcześniejszym artykule mówiłem już czym są bufory. Mówiłem również o mechanizmie ich działania oraz o równaniu Hendersona-Hasselbalcha Teraz przyszedł czas na konkrety – zabieramy się za zadania z buforami! Ale spokojnie, postaram się, żeby było wesoło i zrozumiale, bo przecież chemia to nie tylko kwasy i zasady, ale także solidna dawka humoru!

Przykład 1 – Jak zrobić bufor octanowy i nie wylać?

Załóżmy, że chcesz stworzyć bufor octanowy. Masz pod ręką 50 cm³ kwasu octowego o stężeniu 0,02 M oraz 164 mg octanu sodu. Twoim celem jest obliczenie pcH buforu. Prościzna, prawda? Przyjmijmy, że pKa = 4,55. Teraz zaczyna się zabawa!

Reakcje dysocjacji, czyli kto z kim i dlaczego?

Najpierw musimy napisać równania reakcji dysocjacji obu związków:

CH₃COOH < --> CH₃COO^- + H⁺

CH₃COONa --> CH₃COO^- + Na⁺

Zauważ, że kwas octowy trochę się opiera i nie dysocjuje z wielkim entuzjazmem. Za to octan sodu wchodzi jak boss i dysocjuje w 100%, bo tak to już jest z solami, które mają sód lub potas – nie bawią się w półśrodki! Kwas octowy dysocjuje w niewielkim stopniu, w takim razie w układzie na pewno musi  ustalić się równowaga między tym co zdysocjowało, a tym co nie zdysocjowało. Tego typu równowagę w chemii oznaczamy strzałką z dwoma grotami ( < -- > ) tak jak w pierwszej reakcji.  

Co dalej? Stała dysocjacji

W następnym kroku musimy napisać stałą dysocjacji do pierwszej reakcji.

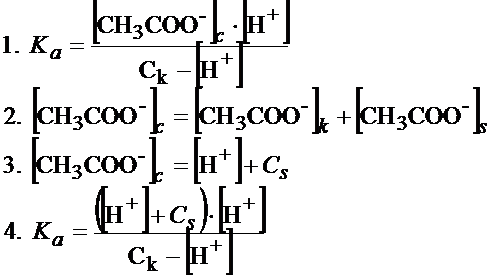
(Uwaga! Reakcja, w której dysocjacja jest 100% nie ustala się żadna równowaga między tym co zdysocjowało a tym co nie zdysocjowało, bo w niej dysocjuje wszystko. Z tego względu do dysocjacji octanu sodu nic piszemy, żadnej stałej dysocjacji).

W liczniku mamy stężenie jonów octanowych. Przyjrzyj się tej naszej mieszaninie, szczególnie na stężenie jonów octanowych, co wypływa? Wypływają oczywiście jony octanowe pochodzące z dysocjacji kwasu octowego, ale również z dysocjacji soli. Tak więc spokojnie możemy napisać:

[CH₃COO^-]_c=[CH₃COO^-]_k + [CH₃COO^-]_s

Jeśli chodzi o jony octanowe pochodzące z dysocjacji kwasu to z reakcji widać, że są one w stosunku 1:1 z jonami wodorowymi, tak więc stężenie jednych i drugich jest dokładnie takie same. Skoro tak, to wymiennie możemy stosować [CH₃COO^-]_k i [H⁺]. Jeśli natomiast chodzi o stężenie jonów octanowych pochodzących od soli to ich stężenie jest dokładnie takie same jak stężenie soli.

[CH₃COO^-]_s=C_s

Możemy więc napisać, że:

[CH₃COO^-]_c=[H⁺] + C_s

A następnie podstawić do pierwszego równania:

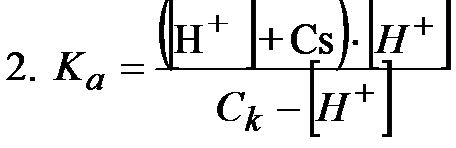
W równaniu 2 można zrobić założenia, dzięki którym uda nam się uprościć to równanie.

Kwas octowy bardzo słabo dysocjuje, jeszcze dodatkowo octan sodu cofa jego dysocjację (reguła przekory), tak więc stężenie jonów [H⁺] jest dużo mniejsze od stężenia soli C_s , więc nie popełnimy dużego błędu jeśli z nawiasu w liczniku usuniemy stężenie jonów wodorowych uznając je za znikomo małe.

[H⁺]<<C_s

Takie same założenie można zrobić do mianownika

[H⁺]<<C_k

Teraz można skrócić równanie nr 2

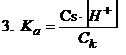
Z tego wzoru można już bez problemu obliczyć stężenie jonów wodorowych, a znając już stężenie jonów wodorowych obliczymy p_cH. Wystarczy tylko pamiętać, że p_cH=-log[H⁺].

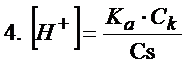
Jest jeszcze tylko jeden mały problem, niestety z treści zadania nie znamy stężenia soli. Tylko czy to jest jakiś problem? A no nie, bo z treści zadania znamy masę octanu sodu oraz objętość. Bez problemu przeliczymy to na stężenie molowe.

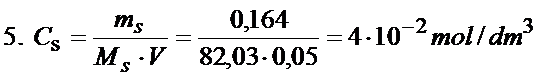
Ok. Mamy już stężenie soli więc możemy skorzystać teraz z równania nr 4 i dokończyć obliczenie stężenia jonów wodorowych.

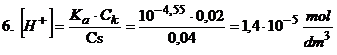
Zbliżamy się już do końca tego zadania. Trzeba jednak jeszcze pamiętać aby na samym końcu sprawdzić czy założenia jakie dokonaliśmy były słuszne. Przyjęło się, że jeśli poniższe stosunki są mniejsze od 1% to założenia jakie dokonaliśmy były słuszne, bo skrócenie wzoru praktycznie nie ma wpływu na wynik końcowy. Uznaje się, że to uproszczenie praktycznie wcale nie wypływa na wynik końcowy.

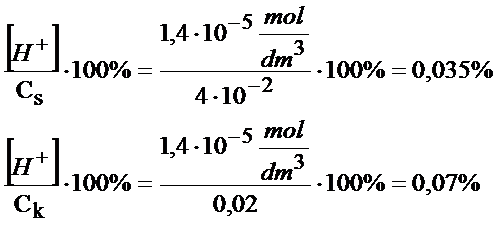
Tak jak widzisz założenia były słuszne, bo te stosunki są mniejsze od 1%, tak więc założenia praktycznie wcale nie miały wpływu na wynik końcowy. Jak już się upieniliśmy, że założenia są ok. to teraz możemy skorzystać ze stężenia jonów wodorowych i  dokończyć obliczenie p_cH

p_cH=-log[H⁺]=-log[1,4*10^-5]=4,85

Przykład 2 – Gra z NaH₂PO₄, czyli co zrobić, żeby pH było 7?

W laboratorium masz dostępne 250cm³ roztworu NaH₂PO₄, w którym liczba moli NaH₂PO₄ jest równa 0,1mol . Oblicz masę Na₂HPO₄ jaką należy dodać aby po dopełnieniu objętości do 1 dm³ p_cH roztworu wynosiło 7. Przyjmij, że pK_a2=6,34, pK_a3=11,3

W przypadku soli rolę kwasu przejmuję ta, która ma więcej protonów.

Dysocjacja i śmieszki z kwasów

Tutaj mamy do czynienia z dysocjacją soli, gdzie jeden związek zachowuje się jak kwas, a drugi jak zasada. Dysocjacje wyglądają następująco:

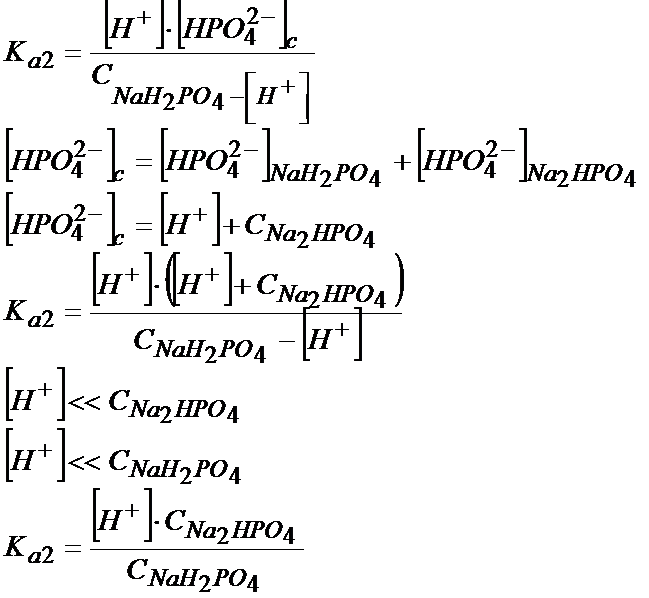
W tym zadaniu zastosowanie założeń wydaje się jak najbardziej słuszne, gdyż stężenie jonów wodorowych ma być równe 10^-7, a więc jest bardzo, bardzo małe. Mamy obliczyć masę soli tak, że musimy przekształcić powyższy wzór i wyciągnąć z niego stężenie soli, a później ze stężenia przejdziemy na liczbę moli, a jak już będziemy mieli liczbę moli to bez problemu obliczymy masę.  Żeby jednak obliczyć stężenie soli to musimy jeszcze znać stężenie kwasu C_NaH2PO4

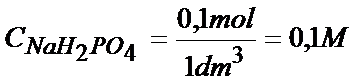
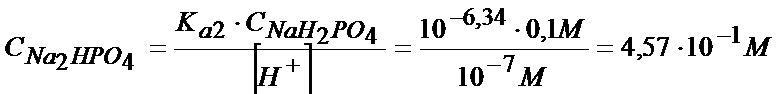
 Znając już stężenie możemy to przeliczyć na ilość moli. Z tym jednak problemu nie będzie, bo objętość roztworu jest równa 1dm³ tak więc liczba moli i stężenie w tym przypadku mają taką samą wartość.

n_Na2HPO4=4,57*10^-1mol

m_Na2HPO4= n_Na2HPO4*M _Na2HPO4=4,57*10^-1mol*142g/mol=70g

Odpowiedź. Żeby pH roztworu było na poziomie 7 to trzeba wprowadzić do układu 70g.

Jeszcze nie rozumiesz buforów? Spokojnie, mam coś dla Ciebie!

Jeśli po tej dawce wiedzy i śmiechu dalej czujesz, że bufor to coś z innej planety, nie martw się! Mam dla Ciebie specjalny kurs „BUFORY”, w którym krok po kroku wszystko wyjaśniam, a do tego dostajesz mnóstwo przykładów do przećwiczenia. Chemia nigdy nie była prostsza! Aż chce się liczyć!